Solid State Class 12 Notes Chemistry Chapter 1

July 19, 2021 October 23, 2024

Introduction

This chapter includes knowledge about the study of various types of solids and different types of forces responsible to bind the particles together, arrangement of unit cells in lattice and packing of lattice points, and Calculation of density of unit cell and unit cell dimensions.

Calculation of packing efficiency of solids, Types of voids, their locations and number of voids in different types of arrangements, Imperfections or common defects in solid-state, and Electrical and magnetic properties of solids are also included in this chapter.

General Characteristics of Solid State

A solid-state is characterised by its lowest compressibility and highest density as compared to a liquid and gaseous state. Constituent particles are packed most closely. This state is distinguished from liquids and gases by their definite size, shape and volume. Solids have considerable mechanical strength, rigidity, very strong inter-particle force of attraction and minimum distance among them.

Due to the strong forces of attraction particles in solid-state do not possess any translatory motion but can only have a vibrational motion about their mean position. Solids have negligible fluidity as compared to liquids and gases. The diffusion of particles of a solid-state is negligible.

Classification of Solids

Solids are classified on the basis of two different parameters i.e.,

Packing of constituent particles
Forces of attraction among constituent particles.

Classification on the basis of packing

1. Crystalline Solids

These are the solids in which the constituent particles (atoms, ions or molecules) are arranged in a regular, three-dimensional orderly arrangement, which gets repeated throughout. Hence, these are also called long-range order solids. Quartz, diamond, Boron Nitride, NaCl, ZnS, CsCl etc.

Properties

Crystalline solids have a sharp melting point, which means they change abruptly into a liquid state at a fixed temperature.
Their nature is Anisotropic which means a few of their physical properties such as mechanical strength, refractive index, electrical and thermal conductivity etc. have different values when measured from different directions, in the same crystal.
On cutting with a knife they give sharp and smooth edges.
They are considered true solids with characteristic enthalpy of fusion.

2. Amorphous Solids

Constituent particles are randomly scattered with, no regular arrangement of particles. Therefore they do not have any definite shape or form. Rubber, glass, plastic etc. are commonly known as amorphous solids.

Properties

If constituent particles are arranged in some orderly manner, then this arrangement does not continue for long distances, hence they are short-range order solids.
They have diffused melting points. It means they soften over a wide range of temperatures instead of melting at a particular temperature only.
They are isotropic by nature. It means due to the random arrangement of particles throughout the values of physical properties such as refractive index, electrical and thermal conductivity etc. will have the same value in all directions.
They form diffused and irregular edges when cut with a sharp knife.
They are called pseudo solids or super cooled liquids, as they have a tendency to flow. They have no definite value of enthalpy of fusion.

Classification on the basis of Nature of Intermolecular Forces

(i) Ionic Solids

There is a regular arrangement of positively and negatively charged ions throughout the solid where ions are held together by strong coulombic or electrostatic forces. These solids are very hard and brittle and have very high melting points. In solid-state, ions are not free to move, hence they are insulators but in a molten state or in the aqueous state, their ions become free to move and become a conductor. Ionic solids have high enthalpies of vaporisation. Ex- LiF, NaCl, KNO₃, MgO, etc.

(ii) Metallic Solids

Metal cores and a sea of mobile electrons are the constituents of metallic solids. Each metal atom contributes one or more electrons to the sea of electrons. These electrons are evenly spread out throughout the crystals and weak forces of attraction or metallic bond binds together kernels and a sea of electrons.

Metallic crystals may be hard as well as soft having moderate enthalpies of fusion. A Mobile sea of electrons is responsible for many properties of metals such as malleability (can be beaten into thin sheets), ductility (can be drawn into wires), metallic lustre, thermal conductivity and electrical conductivity etc. Ex- Copper, Iron, Nickel etc.

(iii) Covalent Solids (Network Solid)

These atoms are bonded together by covalent bond formation throughout the crystal. It means there is a continuous network of covalent bonds forming a giant three-dimensional structure or giant molecule. Covalent bonds are strong and directional in nature. These solids are very hard, brittle and very high melting point. Due to the absence of any free electrons or ions, they are insulators. Their enthalpies of fusion are very high. Ex- Diamond, Graphite, Boron Nitride, Silicon Carbide (SiC) etc.

(iv) Molecular Solids

Their molecules are held together by dispersion forces, London forces, dipole-dipole forces or hydrogen bonds. Either atoms or molecules are bonded together by weak dispersion forces or London forces. These are non-conductor soft solids with low m.p. and low enthalpies of vaporisation. They are volatile in nature hence, at room temperature and pressure they are available in a liquid or gaseous state. Ex- Iodine, Solid H₂ and CO₂ (dry ice). Naphthalene, Camphor etc.

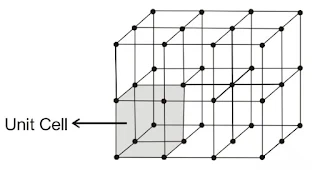
Crystal Lattices and Unit Cells

(i) Crystal Lattices

In a crystalline solid, constituent particles are arranged in a definite, three-dimensional regular geometrical order along all the three axes, in which each particle is depicted as a lattice point. A three-dimensional, regular arrangement of lattice points in space or in a crystal is called a crystal lattice or space lattice.

Crystal lattices have the following characteristics

Each point in the lattice is called a lattice site or lattice point.
Each lattice point represents one constituent particle i.e. atom, ion or molecule.
We join lattice points with straight lines to show the geometry of the lattice.

(ii) UNIT CELL

The smallest repeating unit in space lattice when repeated over and over again in different directions produces a complete crystal lattice. There are two important parameters of a unit cell.

Edge length or Axial Distance: Lengths or dimensions along the three edges a, b and c which may or may not be mutually perpendicular.
Interaxial Angle: Angles α, β and γ between pairs of edges are interaxial angles.
α: between axis B and C
β: between axis A and C
γ: between axis A and B

Types of Unit Cells

Unit cells can be broadly divided into two categories, primitive and centred unit cells.

1. Primitive Unit Cells

When constituent particles are present only in the corner positions of a unit cell, it is called the primitive unit cell.

2. Centred Unit Cells

When a unit cell contains one or more constituent particles present at positions other than corners in addition to those at corners, it is called a centred unit cell. Centred unit cells are of three types:

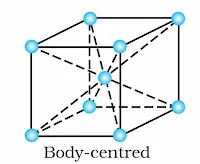
(i) Body-Centred Unit Cells: Such a unit cell contains one constituent particle (atom, molecule or ion) at its body centre beside the ones that are at its corners.

(ii) Face-Centred Unit Cells: Such a unit cell contains one constituent particle present at the centre of each face, besides the ones that are at its corners.

(iii) End-Centred Unit Cells: In such a unit cell, one constituent particle is present at the centre of any two opposite faces besides the ones present at its corners.

Number of Atoms in a Unit Cell

A crystal system is made up of a very large number of unit cells and every lattice point is occupied by one constituent particle i.e., atom, ion or molecule. These particles may be at corners, face-centres and body centres in different unit cells. Each unit cell is adjacent to another unit cell. Most of the atoms are shared by neighbouring unit cells.

In order to calculate the number of points in a unit cell following generalisations can be used.

A point present at the corner of a unit cell is shared by eight other unit cells, therefore its contribution to each unit cell is `1/8`th.
A face is common to two unit cells therefore any point present at the face centre has a contribution of 1/2 to each unit cell.
A point present on each edge-centre is shared among four unit cells therefore its contribution to each unit cell is `1/4`.
A point present at the centre of the body of the unit cell has a complete share of one, as it is not shared with any other unit cell.

By using this information, let us calculate the number of constituents or atoms per unit cell.

(i) Primitive Cubic Unit Cells:

In this cell, particles are present only at 8 corners and an atom from each corner contributes `1/8` th.

∴ Total number of atoms per unit cell = `1/8\times 8` = 1 atom

Body-Centred Cubic Unit Cell:

It has 8 points at the 8 corners and one point at the body–centre of the cube.

∴ Total number of atoms per unit cell = 1 + 1 = 2

Face-Centred Cubic Unit Cell:

There are 8 points at the corners and 6 points at 6 face centres of each unit cell.

Therefore, the Number of atoms from 8 corners of the unit cell = `1/8\times 8` = 1

Number of atoms from 6 face centres = `1/2\times 6` = 3

∴ Total number of atoms per unit cell = 1 + 3 = 4.

Close Packed Structures

Let us consider all the constituents are identical to solid spheres. In a two-dimensional arrangement, spheres are arranged in rows to form a layer and packed in different layers to form a three-dimensional arrangement which is known as crystal or space lattice.

(a) Close packing in one Dimension: Arrangement of different atoms in a row touching each other forms one dimension or edge. The coordination number is 2.

(b) Close packing in two-Dimensions: The rows of particles can be stacked in two ways:

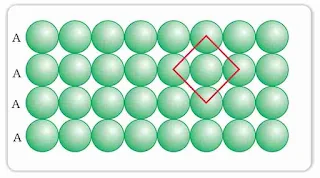
Square Close Packing: Spheres are packed in such a way that they align together vertically as well as horizontally and the centre of all spheres is in a straight line. Here each sphere is in contact with four other spheres in the same plane. This is termed as square close packing and the coordination number is 4.

Hexagonal close Packing: When the second row is arranged in the depressions of the first row and all atoms align diagonally to each other. Each atom is in contact with 6 other spheres in the same plane. It is known as hexagonal close packing. It is a more efficient mode of packing than the square close packing in a layer in two dimensions. Here the co-ordination number is 6. In this layer triangular voids are formed.

(c) Close Packing in three Dimensions: When layers are arranged over each other they form three-dimensional packing. It is layer packing in which the second layer is placed over the first layer in such a way that all the spheres are exactly above each other and all the spheres align horizontally as well as vertically. This arrangement forms AAA ........ type of lattice. It forms a simple cubic lattice and its unit cell is a primitive cubic unit cell.

Tetrahedral voids are holes or voids surrounded by four spheres Present at the corner of a tetrahedron. The coordination number of a tetrahedral void is 4.

Octahedral voids are holes surrounded by six spheres located on a regular tetrahedron. The coordination number of the octahedral void is 6.

In ccp or hcp the number of octahedral voids present in the lattice is equal to the number of lattice points and the number of tetrahedral voids is twice the number of lattice points.

Packing Efficiency

In all the types of packings, there is always some free space in the form of voids or vacant spaces. Packing efficiency is the percentage of total space filled by the particles.

Packing efficiency = Volume of total lattice points / Total volume of unit cell

(i). Packing efficiency in fcc or ccp structures

suppose edge length of unit cell = a

And radius of sphere = r

In ΔABC, AC² = BC² + AB²

AC² = a² + a²

AC² = 2a²

Hence, face diagonal AC = `\sqrt{2}`a

But AC = 4r `\therefore 4r=\sqrt{2}a \therefore a=frac{4r}{\sqrt{2}}`

Hence, volume of unit cell = `a^3` or

`a^3=(\frac{4r}{\sqrt{2}})=16\sqrt{2}r^3`

As there are total 4 lattice points per unit cell.

Packing efficiency = `\frac{4\times 4/3\pi r^3}{16\sqrt{2}r^3}`

= `\frac{16\pi r^3}{3\times 16\sqrt{2}r^3}`

= `\frac{\sqrt{2}\pi}{6}=0.74`

Hence, % Packing efficiency = 74%

(ii). Packing Efficiency in bcc structures

Suppose the edge length = a

Radius of each sphere = r

Number of lattice points per unit cell = 2

In ΔABC, AC² = BC² + AB² = a² + a² = 2a²

Similarly in ΔACD,

AD² = AC² + CD² = 2a² + a² = 3a²

AD = `\sqrt{3}`a

Now, AD = 4r `\therefore\sqrt{3}a=4r or a=\frac{4r}{\sqrt{3}}`

Packing efficiency = `\frac{2\times\frac{4}{3}\pi r^3}{(\frac{4r}{\sqrt{3}})^3}`

`=\frac{8\pi r^3\times 3\sqrt{3}}{3\times 64r^3}`

`=\frac{\sqrt{3}\pi}{8}=0.68`

Hence, % of Packing efficiency = 68%

(iii). Packing Efficiency in Simple Cubic Unit Cell

Let the edge length of the unit cell = a

The radius of sphere = r

As two spheres touch each other at an edge

`\therefore a=2r`

Number of lattice points per unit cell = 1

Packing efficiency = `\frac{4/3 \pir^3}{(2r)^3}=\frac{\pi}{6}=0.524`

Hence, % Packing efficiency = 52.4%

Calculation for Unit Cell Dimensions

Let the edge length of a cubic crystal of an element or compound = a cm

The volume of unit cell = a³ cm³

The density of unit cell = Mass of unit cell / Volume of the unit cell

Mass of unit cell = Z × m.

Here Z is the number of atoms present in one unit cell and m is the mass of a single atom.

m = Molar mass / Avogadro's number

`m=\frac{M}{N_0}`

Mass of unit cell = `Z\times\frac{M}{N_0}`

Density (ρ) = `\frac{Z\times M}{N_{0}\times a^3}`

Imperfections in Solids

Irregularities in the arrangement of constituent particles in the crystalline state are called imperfections or defects. Generally, defects arise during crystallisation processes at a fast or moderate rate.

Point defects are the irregularities or deviations from ideal arrangement around a point or an atom in a crystalline substance, whereas line defects are the irregularities or deviations from the ideal arrangement in entire rows of lattice points. These irregularities are called crystal defects.

Types of Point Defects

(i). Vacancy defect

When some of the lattice sites are vacant, the crystal is said to have vacancy defects, which results in a decrease in the density of the substance. This defect can also develop when a substance is heated.

(ii) Interstitial defect

When some constituent particles (atoms or molecules) occupy an interstitial site, the crystal is said to have an interstitial defect. This defect increases the density of the substance. Such types of defects can be shown by non-ionic solids. Ionic solids must always maintain electrical neutrality, to show Frenkel defects and Schottky defects.

(iii) Schottky Defect

In ionic solids, some cations and a proportionate number of anions are missing from the lattice. While doing so electrical neutrality of the solid is not disturbed. It is termed a Schottky defect. The solids having comparable cationic and anionic radii where the Coordination number is high, generally show this defect. Highly ionic substances such as NaCl, KCl, CsCl, CsBr etc. show this defect. Due to this defect density and stability of the solid decrease while its electrical conductivity increases.

(iv) Frenkel Defect or Dislocation Defect

In some ionic solids smaller ions usually, cations are dislocated from their normal site to some interstitial site. It is termed a Frenkel defect. Ionic substances having large size variation between cation and anion and low Co-ordination numbers generally show this defect e.g., ZnS, AgCl, AgBr, AgI etc.

F-Center

When there is an excess of metal ions in non-stoichiometric compounds, the crystal lattice has vacant anion sites. These sites are occupied by electrons. These anion sites occupied by electrons are called F-centres.

Electrical Properties

On the basis of conductivity, solids are classified as conductors, semiconductors and insulators.

Mechanism of Electrical Conduction

The atomic orbitals of metal atoms form molecular orbitals which together form a band. The outermost filled energy band is the valence band and the next empty band in which electrons can move is called the conduction band.

In metals, the conduction band is close to the valence band and therefore electrons can easily move to the conduction band. Therefore they are good conductors.
If the gap between valence and conduction band is very large, electrons can't jump hence they behave as insulators.
In semiconductors, there is a small energy gap between valence and conduction band therefore some electrons can jump to the conduction band and show some conduction. On heating electrons can jump from the valence band hence these types of conductors are called intrinsic semiconductors.

The conductivity of Intrinsic semiconductors is very low which can be increased by adding the appropriate amount of suitable impurity to it. This is called doping. It means when some impurity is added to Si or Ge they can be converted to semiconductors. This doping may be of two types.

(i). n-type semiconductors

When an element of group-14 i.e. Si or Ge having 4 valence electrons are mixed with some quantity of group 15 element such a 'P' or 'As' having 5 valence electrons. They together form 4 covalent bonds and the 5th valence electron on 'P' or 'As' remains unbonded and delocalised. These delocalised electrons increase the conductivity of doped Si or Ge. As an increase in conductivity is due to the negatively charged electrons, hence these types of semiconductors are called n-type semiconductors.

(ii). p-type semiconductors

When elements of group-14 i.e. Si or Ge having 4 valence electrons are doped with the elements of the group–13 elements i.e. B or Al having 3 valence electrons, 3 covalent bonds are formed. The place where the fourth valence electron is missing is called electron-hole or electron vacancy. An electron from a neighbouring atom can come and fill the electron-hole but it leaves a hole at its original position. In this way, electrons and holes seem to be moving in opposite directions and cause the conductivity of substances. These are called p-type semiconductors

Magnetic Properties

Magnetic properties of materials are due to magnetic moments associated with the individual electron. The magnetic moment of each electron may originate from any of the two types of motion.

Orbital motion around the nucleus
Spin of an electron around its own axis

A moving electron is considered as a small current loop which generates a small magnetic moment along its axis of rotation as a magnetic moment which originates from electron spin and is directed along the spin axis. Each electron in an atom is considered a small magnet having a permanent orbital magnetic moment and spin magnetic moment. The fundamental magnetic moment is Bohr Magneton μ_B which is equal to 9.27 × 10^–24 Am². They are classified into 5 types.

Diamagnetic Material: The solids having all the paired up electronic spins are diamagnetic. They are weakly repelled by the magnetic field e.g. NaCl, C₆H₆, H₂O etc.
Paramagnetic Substances: They have permanent magnetic dipoles due to a few unpaired electronic spins i.e. 1, 2, or 3 and they are weakly attracted by the applied magnetic field but cannot be magnetised permanently e.g. Cu⁺², Fe⁺³, O₂, CuO, TiO, VO₂ etc.
Ferromagnetic Substances: These substances cannot only be attracted by magnets strongly, rather they can be permanently magnetised as well. Metal ions of ferromagnetic substances are in solid-state grouped together into small regions called domains. Each domain acts as a tiny magnet. In the external magnetic field, these domains get oriented in the direction of the magnetic field. On the alignment of magnetic moments of domains in substance, we observe that
- When there is the spontaneous alignment of magnetic moments of domains in the same direction, they become ferromagnetic substances e.g. Fe, Co, Ni, CrO₂ .
- If magnetic moments are aligned in a compensatory way so that they all cancel out each other and the net magnetic moment becomes zero, these are antiferromagnetic substances e.g. MnO.
- When magnetic moments of domains are aligned in parallel and antiparallel directions in unequal numbers, it results in some net magnetic moment. These are ferrimagnetic substances. These are weakly attracted by magnetic fields e.g. Fe₃O₄, MgFe₂O₄, ZnFe2O4 etc.

Summary

Crystalline solids: Substances having a definite and orderly arrangement of constituent particles through the whole lattice are crystalline solids e.g. diamond, ZnS etc.
Amorphous solids: Substances not having any geometrical arrangement of constituents but rather a scattered arrangement of particles are amorphous by nature. e.g. Rubber, glass etc.
Molecular solids: Made up of molecules which may interact with each other by van der Waals forces, hydrogen bonding, dipole-dipole interactions etc e.g. solid CO₂, wax, iodine etc.
Ionic solids: Having cations and anions as constituent particles and coulombic forces as forces of interaction e.g., NaCl, CsCl, ZnS etc.
Lattice point: Smallest atoms or ions present in a solid which constitute the solid are lattice points.
Crystal lattice: It is a regular arrangement of constituent particles of a crystal in three-dimensional space.
Unit Cell: The smallest three-dimensional portion of the space lattice which forms a whole crystal lattice when repeatedly arranged in three dimensions.
Simple or primitive cubic unit cell: Having atoms or ions only at the corners of the unit cell.
Body-Centred cubic unit cell: It has lattice points at 8 corners and one at the body centre of the unit cell.
Face-Centred cubic unit cell: It has 8 lattice points at 8 corners and 6 lattice points at 6 face centres.
End-Centred: In addition to the 8 lattice points at 8 corners, there is one particle each at the centre of two opposite faces.
Coordination number: The coordination Number of any particle is equal to the number of its closest neighbours.
Hexagonal close packing (hcp): It is three dimensions of layerwise close packing of constituent particles called ABAB ..... type packing in which every 3rd layer is the same as the first layer.
Cubic close packing (ccp): It is three-dimensional layerwise close packing of constituent particles called ABCABC ... type packing in which every fourth layer is the same as the Ist layer.
Voids or holes: Some vacant or unoccupied spaces available in ccp or hcp are called voids or holes.
Tetrahedral Voids (T.V.): A triangular void, surrounded by four spheres arranged tetrahedrally around it is Tetrahedral voids. Its Coordination number is 4.
Octahedral Void (O.V.): A double triangular void surrounded by total of six spheres making it like an octahedron. Its Co-ordination Number is 6.
Schottky defect: Equal or proportionate number of cationic and anionic vacancies, causing a decrease in density of solid.
Frenkel defect: Dislocation of certain cations to some interstitial voids is called Frenkel defect. The density of solid remains unchanged.
F-centres: Sites from where anions are missing from lattice and the vacant holes are occupied by free electrons. These are responsible for the conductance and colour of solids.
Doping: The addition of a small amount of foreign impurity to a crystal is called doping. It helps in increasing the conductivity of solids.
Diamagnetic substances: Substances containing no unpaired electronic spins and which are weakly repelled by a magnetic field are diamagnetic e.g. Ne, Ar, Ca⁺², Na⁺ etc.
Paramagnetic substances: Which are weakly attracted by the magnetic field and have 1, 2 or 3 unpaired electronic spins e.g. O₂ etc.
Ferromagnetic substances: These substances have permanent magnetism even in the absence of a magnetic field. They have 3, 4, or more unpaired electronic spins. e.g. Fe, Ni, Co etc.
Antiferromagnetic substances: Ferromagnetic substances in which magnetic moment becomes zero due to alignment of unpaired electronic spins under the applied magnetic field e.g. FeO, MnO etc.
Ferrimagnetic substances: Ferromagnetic substances show small paramagnetic behaviour due to unequal alignment of unpaired electronic spins in opposite directions e.g. Fe₃O₄ etc.

Read also

Class 12 (Chemistry)